Increasing extreme hourly precipitation risk for New York City after Hurricane Ida – Scientific Reports

Contextualizing Ida historically

The annual maximum warm-season (May 1st to October 31st) hourly rainfall time series for the Central Park rain gauge, or extreme rainfall intensity (R hereafter), is first examined in Fig. 2a. This figure shows that the extreme precipitation of 2021 associated with Hurricane Ida (3.47 inches (88.1 mm) per hour) was about 75% greater than the previous highest annual warm season intensity of 1.95 inches (49.5 mm) per hour in 1995. It is also twice the magnitude of the design rainfall of 1.75 inches (44.5 mm) per hour used by NYC to size its drainage system. An evident trend (0.05 in/hr/decade, or 1.3 mm/hr/decade) over 1948–2023 is statistically significant at the 5% rejection rate. There is no significant auto-correlation in the time series, and the statistical significance of the trend is also tested using a bootstrap resampling approach that considered Ida-like event occurrence in any year between 1948 and 2023 (see “Methods” section and Supplemental Figure S1).

A time-evolving Mann-Kendall trend test is conducted to investigate this trend more systematically. Mann-Kendall trend test’s p-value is estimated beginning with the first 31 years (1948–1979). Subsequently, the dataset is updated by adding one year each time (e.g., 1948–1980, 1948–1981, …, 1948–2022, 1948–2023) and the Mann-Kendall trend test’s p-value is re-estimated. The temporal tendency of this p-value (computed each time based on an updated time series of extreme rainfall intensity) indicates the variable nature of the trend in extreme rainfall intensity. Figure 2b presents these results and shows how the trend significance has evolved since record-keeping began at Central Park. A statistically significant increase in extreme rainfall intensity (as determined by p-value 2b. A conjunction of the time series of extreme rainfall intensities (Fig. 2a) and the tendency of the Mann-Kendall trend significance (Fig. 2b) indicates that the extreme rainfall intensity has been trending post-2000s upwards and amplified since 2018 (overall, 0.05 in/hr/decade as seen in 2a, or 1.3 mm/hr/decade), highlighting the already-changing nature of extreme rainfall intensity in NYC. Figure 2a also presents three regression lines over varying periods of 1948–2023, 1948–2000, and 1948–1992 to gauge the range of the trend amongst high variability. The blue and red lines show a significant trend; 1948–1992 (blue) is the period of the first significant trend, and 1948–2023 (red) capturing the overall trend. The third yellow line (1948–2000) shows the year with the most statistically insignificant trend, primarily due to a multi-year period of low rainfall intensities that followed the 1990s.

Figure 2c presents the temporal evolution of the return period (or mean recurrence interval) of Ida’s rainfall intensity of 3.47 inches (88.1 mm) per hour. After significance testing of parameters, Gumbel distribution (Type I Extreme Value Distribution as a natural distribution for block maxima³⁵) was chosen to represent extreme rainfall intensity data best. Like the analysis conducted in Fig. 2b, the return period of Ida’s rainfall intensity is estimated using yearly-updated rainfall intensity. When the return period of Ida’s rainfall intensity is estimated using a Gumbel distribution fit to extreme rainfall intensity data from 1948 to 1979, it is approximately a 7,500 year-storm. Subsequently, the Gumbel distribution parameters are re-estimated using updated rainfall intensity data each year, and the return period is computed to obtain the tendency of the return period of Ida’s rainfall intensity of 3.47 inches (88.1 mm) per hour. When the full data record, which includes the 2021 Ida event, is used (1948–2023), the return period is approximately 2500 years. Figure 2c also shows a locally-weighted polynomial trend line using a smoothing span of 0.5³⁶ to highlight the tendency of the return period of Ida. The extreme rainfall intensity already had a significant uptrend before the 2021 Ida event (Fig. 2b), and the return period of an Ida-like event has been decreasing (or the likelihood of the event was increasing) even before Ida happened (Fig. 2c). It is to be noted that even with the return period dropping by half, the Ida event still has an extremely low probability of occurrence. The changing likelihood or probability of an Ida-like event further motivates the need for a formal nonstationary modeling framework to project the risk due to such extremely low-probability high-impact events in the future.

Non-stationary and stationary approaches for risk assessment

Traditional precipitation frequency analysis assumes stationarity of the parameters of the probability distributions, resulting in static estimates for hazards or the probability of extreme events. However, since precipitation frequency, accumulation, and intensity are increasing (or changing over time), the magnitude and likelihood of any n-year storm would also vary dynamically. A lack of adequately long data records to correctly estimate the time-varying parameters in a nonstationary realm and an understanding of how the climate will evolve under global warming limits nonstationary usage. Given the temporal evolution of the trend and the likelihood of an Ida-like event observed in Fig. 2c, stationary and nonstationary modeling approaches were developed to project the probability of a storm of Ida’s magnitude. This framework also enables comparisons between stationary and nonstationary approaches for extreme rainfall intensity prediction and subsequent stormwater management for urban areas.

We use Gumbel-based models to quantify the future probability of an Ida-like event under stationary and nonstationary assumptions (model formulation details are presented in the “Methods” section). Under a stationary assumption, extreme rainfall intensity is modeled as a Gumbel distribution with time-invariant parameters. The future probability of an Ida-like event is a fixed annual exceedance probability estimated from the model and, hence, static for any future planning phase. This model’s location and scale parameters are 0.958 and 0.326, respectively (in units of inches per hour, or 2.43 and 0.83 mm per hour), and the static probability of an Ida-like event (\({p}_{s}\)) is 0.045%.

The nonstationary models are distinguished by the time varying parameters for the Gumbel distribution. Each model’s parameters are estimated respectively each year using covariates of time for non-stationary model 1 (Eq. 8), and higher (SSP 370) and lower (SSP 126) emission scenario model simulations^{37,38,39,40,41} of \({T}_{avg}\) and it’s integral over 65 ℉ (Cooling Degree Days, or CDD – see Eq. 1) for non-stationary models 2 and 3 (Eqs. 9 and 10). Such non-stationary methods have been applied to precipitation in other regions^17,18,33,42 including an evaluation of regionally appropriate covariates⁴³. Its value and application as a tool for extreme precipitation under climate change is now well established (see for example, review articles by Yuan et al., Wright et al., Slater et al., and Schlef et. al^44,45,46,47).

To project the future probability of an Ida-like event, we have developed two versions of the model: one that uses \({T}_{avg}\) projections and one that uses CDD projections. These are obtained by using the air temperature data from two warming scenarios from a single grid cell covering NYC from three models: GFDL-ESM4.1³⁷, CESM2³⁸, and MPI-ESML1-2-HR^40,41. Each of the models have: (1) a nominal resolution of 100 km, (2) historical simulations that go back to the start of central park’s hourly precipitation observations, and, (3) future projections that are at least 50 years past 2023. The projections are adjusted for grid-to-point resolution based on the difference between historical simulations and observations (see “Methods” section and Table 1 for details).

The observational and projected \({T}_{avg}\) data is seen in Fig. 3. The observational data is seen to have a modest positive correlation with extreme rainfall intensity, R, (panel A). A similar correlation is found with CDD (see Supplemental Figure S2 and S3). In 3b, we can see the historical observations over time in relation to all 6 model projections for \({T}_{avg}\). The projections are noisy, and divergences between SSP 126 and SSP 370 are not clearly seen until after roughly the 25-year design period.

\({T}_{avg}\) and CDD are very similar in the historical period in terms of linear trend, correlation with extreme rainfall intensity, and appear visually similar (See Supplemental Fig. 2). However, the nonstationary model coefficients of the location and scale parameters of the Gumbel distribution fit to extreme rainfall intensity, R, conditioned on \({T}_{avg}\) and CDD in the historical period pick up on the differences, and the divergence between these model-dependent time-varying location and scale parameters grow in the future period (see Supplemental Figure S4 and S5). Supplemental Table T1 contains the model coefficients of the parameters from Eqs. (9) and (10) when both covariates are normalized (i.e., converted to standardized anomalies), and this unitless comparison shows that CDD has a larger slope in the scale parameter, and \({T}_{avg}\) has a larger slope in the location term. The difference in the parameters combined with the future projections induce differences in the future probabilities of an Ida-like event. This difference is illustrated in Supplemental Figure S6, where the distribution of simulated extreme rainfall intensity is compared between covariates for one scenario.

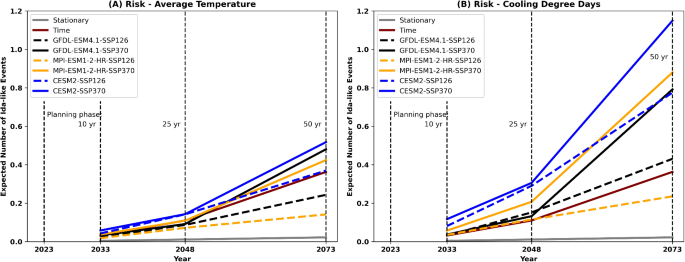
The stationary and nonstationary future probabilities of an Ida-like event are used in a decision tree framework (see Eqs. 11–15 in the “Methods” section and Supplemental Figure S7) to derive the expected future risk of such extreme rainfall intensities over three specific planning phases that the city planners and engineers often consider for operation and design of hydraulic infrastructure – a 10-year immediate timeframe risk, a 25-year intermediate timeframe risk, and a 50-year long-term risk. Figure 4 presents these results for all the developed models (M0, M1, M2, M3, respectively Eqs. 7, 8, 9, 10), with each climate model’s high and low scenario run with M2 and M3 (Eqs. 9 and 10). The risk presented is aggregated over time, but it is important to note the \({T}_{avg}\) and CDD driven models (M2 and M3) show non-linear risk change with time. Yearly probabilities for future 10 years from select models are shown in Supplemental Table T2.

The range of the number of expected Ida-like events in the next 10, 25, and 50 years. All probabilities are calculated yearly for the 3 design periods onwards from 2024, and then aggregated using a decision tree. Analysis is the same for both panels with the exception of covariate choice. Stationary refers to M0, Time refers to M1, and the rest use the climate covariate-specific M2/3 (see methods for details). Asides from the stationary line, all the results are non-stationary models.

Substantial differences are realized between stationary future risk and nonstationary future risk across the three planning phases, as well as between models with \({T}_{avg}\) and CDD as covariates. For a 10-year immediate timeframe, the expected risk of an Ida-like event is 0.4% under a stationary climate assumption. However, the anticipated risk under nonstationary assumptions ranges from 4 to 13 times when using \({T}_{avg}\) and 7–26 times the stationary risk for the same 10-year design period when using CDD. These risk ratios are higher for the 25- and 50-year timeframes, with the 50-year long-term risk being as high as 115% under the CDD-driven high-emission (SSP 370) scenario of the CESM2 climate model, or 52 times greater than the stationary estimate (2% over 50 years). In the most extreme case, the expected number of Ida-like extreme rainfall intensity events over the next 50 years is more than 1 occurrence (115%) if one uses the CESM2 high-emission scenario-based CDD to project extreme rainfall intensities, and 52% when using \({T}_{avg}\). The 50-year planning phase shows a great deal of variability in the probabilities, depending on which climate model, scenario, and covariate is used, indicating that there is large uncertainty in these risk ratio estimates. However, even when variability across the model is accounted for, all the non-stationary models return results much larger than the stationary risk.

That the CESM2 model provided the highest probabilities is consistent with its relatively higher Equilibrium Climate Sensitivity compared to the other two models. At the 25-year planning phase, each climate model shows a different relationship between their high and low scenario predictions. For example, the GFDL ESM4.1 low emission scenario indicates a higher risk than its high emission counterpart because the CDD from both scenarios is relatively similar at that point. This reflects the variability of \({T}_{avg}\) (and CDD) projections in Fig. 3b (and Supplemental Figure S3), and that a large divergence in scenarios is not seen for decades after the projection initialization.

These expected risk estimates can readily translate into equivalent annualized costs or damages the city might incur. While the nonstationary models clearly project a greater number of Ida-like events than the stationary assumption, it is to be noted that these are based on stochastic projection models that factor in the observed trends in extreme precipitation. These trends do not differentiate between storm type nor do they incorporate specific knowledge about the underlying atmospheric dynamics. Hence, the results must be viewed from a risk assessment lens, not a deterministic viewpoint.